Gone Too Young: The Impact of Food, Sleep, and Income on Premature Mortality

Author

Sarah Grabinski

Published

December 11, 2022

Preliminaries

My Packages

# RMarkdown Packages
library(knitr)
library(rmdformats)

# Global options
options(max.print="150"); opts_chunk$set(comment=NA); opts_knit$set(width=75)

# Packages used in this project
library(broom)
library(equatiomatic)
library(patchwork)
library(ggrepel)
library(kableExtra)
library(janitor)
library(naniar)
library(tidyverse)

# Set theme for plots
theme_set(theme_bw())

Data Ingest

This project uses the 2022 CHR CSV Analytic Data from the County Health Rankings.

data_url <- 
  "https://www.countyhealthrankings.org/sites/default/files/media/document/analytic_data2022.csv"

# Read in CSV from the URL, skip the header row, use up to 4000 rows
# to guess column types, do not show the guessed column types
chr_2022_raw <- read_csv(data_url, skip = 1, guess_max = 4000, 
                         show_col_types = FALSE)

Data Development

Selecting My Data

I filtered my data for ranked counties in the states of Ohio, Florida, Illinois, and Tennessee and selected my variables of interest. I gave them more meaningful names than the original v-codes, scaled the proportions to percentages, and scaled the income to thousands of dollars.

chr_2022 <- chr_2022_raw |>
  # Use only ranked counties from Ohio, Florida, Illinois, and Tennessee
  filter(county_ranked == 1,
         state %in% c('OH', 'FL', 'IL', 'TN')) |>
  # Select the raw variables
  select(fipscode, state, county, county_ranked,
         v127_rawvalue, # premature death / years of life lost
         v139_rawvalue, # proportion of county experiencing food insecurity
         v143_rawvalue, # proportion of county experiencing insufficient sleep
         v168_rawvalue, # proportion of county that has completed high school
         v063_rawvalue # median income of county in dollars
         ) |>
  # Give the variables new, meaningful names
  rename(years_lost = v127_rawvalue, # outcome
         food_insecurity = v139_rawvalue, # quantitative predictor 1
         insufficient_sleep = v143_rawvalue, # quantitative predictor 2
         hs_completion_raw = v168_rawvalue, # binary predictor
         median_income_raw = v063_rawvalue, # categorical predictor
         ) |>
  # Re-scale variables where necessary
  mutate(food_insecurity = food_insecurity * 100, # converts to %
         insufficient_sleep = insufficient_sleep * 100, # converts to %
         hs_completion_raw = hs_completion_raw * 100, # converts to %
         # converts to thousands of $
         median_income_raw = median_income_raw / 1000)

Repairing the `fipscode` and factoring the `state`

The fips code is a 5-digit identifier that was converted to a numeric variable on import. I repaired it by adding back any leading zeros that were stripped, and I converted the state to a factor.

chr_2022 <- chr_2022 |>
  mutate(fipscode = str_pad(fipscode, 5, pad = "0"),  # repair the fips code
         # factorize state and make Ohio the baseline
         state = fct_relevel(factor(state), 'OH', 'IL', 'FL', 'TN'))

Creating a Binary Categorical Variable

I created a tibble of all ranked counties in the US to use in establishing the categorical variables levels based on national averages.

# Create a tibble of all ranked counties in the US
chr_2022_ranked <- chr_2022_raw |>
  filter(county_ranked == 1) |>
  # Select the raw variables
  select(fipscode, state, county, county_ranked,
         v127_rawvalue, # premature death / years of life lost
         v139_rawvalue, # proportion of county experiencing food insecurity
         v143_rawvalue, # proportion of county experiencing insufficient sleep
         v168_rawvalue, # proportion of county that has completed high school
         v063_rawvalue # median income of county in dollars
         ) |>
  # Give the variables new, meaningful names
  rename(years_lost = v127_rawvalue, # outcome
         food_insecurity = v139_rawvalue, # quantitative predictor 1
         insufficient_sleep = v143_rawvalue, # quantitative predictor 2
         hs_completion_raw = v168_rawvalue, # binary predictor
         median_income_raw = v063_rawvalue, # categorical predictor
         ) |>
  # Re-scale variables where necessary
  mutate(food_insecurity = food_insecurity * 100, # converts to %
         insufficient_sleep = insufficient_sleep * 100, # converts to %
         hs_completion_raw = hs_completion_raw * 100, # converts to %
         # converts to thousands of $
         median_income_raw = median_income_raw / 1000)

From the tibble of all ranked US counties, I calculated the national median high school completion percentage (us_median_hs_completion = 88.78%) from hs_completion_raw and used this as a cut point to establish ‘Above Average’ and ‘Below Average’ high school completion categories for my sample.

# Calculate the median high school completion percentage
us_median_hs_completion = median(chr_2022_ranked$hs_completion_raw)

# Use this value to split variable into above and below average categories
chr_2022 <- chr_2022 |>
  mutate(hs_completion_cat = factor(case_when(
    hs_completion_raw < us_median_hs_completion ~ "Below Average",
    TRUE ~ "Above Average"))) |>
  # Reorder the the levels based on median value
  mutate(hs_completion_cat = fct_reorder(hs_completion_cat, 
                                         hs_completion_raw, median))

# Summarize the categories
mosaic::favstats(data = chr_2022, hs_completion_raw ~ hs_completion_cat) |>
  mutate(percent = scales::percent(n/nrow(chr_2022), accuracy = 0.1)) |>
  select(hs_completion_cat, n, percent, median, mean, min, max) |>
  kbl(col.names = c('Category', 'n', 'Percent', 'Median', 
                    'Mean', 'Minimum', 'Maximum'), 
      digits = 2, align = 'c', 
      caption = 'Percentage High School Completion by Category') |>
  kable_classic(full_width = FALSE)

Percentage High School Completion by Category
Category	n	Percent	Median	Mean	Minimum	Maximum
Below Average	176	50.0%	84.94	83.85	56.14	88.77
Above Average	176	50.0%	91.53	91.53	88.80	96.82

Creating a Multi-Category Variable

From the tibble of all US ranked counties, I calculated tertiles from median_income_raw and used these cut points (cut1 = 50.397 thousands of dollars, cut2 = 60.754 thousands of dollars) to establish ‘Low’, ‘Average’, and ‘High’ median income categories.

# Use the previously made tibble of all ranked US counties 
# to calculate cut points for 3 equal quantiles
cut1 = quantile(chr_2022_ranked$median_income_raw, 
              probs = 0.333, na.rm = TRUE, names = FALSE)

cut2 = quantile(chr_2022_ranked$median_income_raw, 
              probs = 0.667, na.rm = TRUE, names = FALSE)

# Use these cut points to split column into low, average, and high categories
chr_2022 <- chr_2022 |>
  mutate(median_income_cat = factor(case_when(
    median_income_raw < cut1 ~ "Low",
    median_income_raw < cut2 ~ "Average",
    TRUE ~ "High"))) |>
  # Reorder the levels based on median value
  mutate(median_income_cat = fct_reorder(median_income_cat, 
                                         median_income_raw, median))

# Summarize the categories
mosaic::favstats(data = chr_2022, median_income_raw ~ median_income_cat) |>
  mutate(percent = scales::percent(n/nrow(chr_2022), accuracy = 0.1))  |>
  select(median_income_cat, n, percent, median, mean, min, max) |>
  kbl(col.names = c('Category', 'n', 'Percent', 'Median', 
                    'Mean', 'Minimum', 'Maximum'), 
      digits = 3, align = 'c', 
      caption = 'Median Household Income by Category') |>
  kable_classic(full_width = FALSE)

Median Household Income by Category
Category	n	Percent	Median	Mean	Minimum	Maximum
Low	119	33.8%	46.080	45.646	32.163	50.297
Average	117	33.2%	55.128	55.359	50.626	60.715
High	116	33.0%	68.008	70.645	60.779	118.257

Revise order of variables

I relocated the county_ranked column to the end of the tibble so that the primary variables print more clearly. I also applied clean_names() to ensure I had unique and clearly formatted variable names.

# Move county_ranked to the end and make sure column names are clean
chr_2022 <- chr_2022 |>
  relocate(county_ranked, .after = last_col()) |>
  clean_names()

Three Important Checks

Missingness

None of my variables are missing any values, so my data set meets the requirement that it must have data for at least 75% of the counties in each state.

# Use naniar to summarize missing values
chr_2022 |> 
  miss_var_summary() |>
  mutate(pct_miss = scales::percent(1-pct_miss)) |>
  kbl(col.names = c('Variable', '# Missing', '% Complete'), 
      align = c('l', 'c', 'c'), 
      caption = 'Missingness Summary') |>
  kable_classic(full_width = FALSE, 'striped')

Missingness Summary
Variable	# Missing	% Complete
fipscode	0	100%
state	0	100%
county	0	100%
years_lost	0	100%
food_insecurity	0	100%
insufficient_sleep	0	100%
hs_completion_raw	0	100%
median_income_raw	0	100%
hs_completion_cat	0	100%
median_income_cat	0	100%
county_ranked	0	100%

Distinctiveness

My variables have between 113 and 352 distinct values each, so my data set meets the requirement of having at least 10 distinct non-missing values per variable.

# Count distinct cases for all variables
chr_2022 |> 
  summarise(across(years_lost:median_income_raw, ~ n_distinct(.))) |>
  kbl(caption = 'Number of Distinct Values', 
      align = c('c', 'c', 'c', 'c', 'c')) |>
  kable_classic(full_width = FALSE)

Number of Distinct Values
years_lost	food_insecurity	insufficient_sleep	hs_completion_raw	median_income_raw
352	113	352	352	351

Category Factor Completeness

The categories of my categorical variables have between 116 and 176 counties per level, so my data set meets the requirement that every level of the factor for categorical variables must include at least 10 counties.

# Use tabyl to count the counties per binary category level
chr_2022 |> tabyl(hs_completion_cat) |>
  adorn_pct_formatting() |>
  kbl(col.names = c('High School Completion Category', 
                    '# of Counties', 'Percent'), align = 'lcc') |>
  kable_classic(full_width = FALSE)

High School Completion Category	# of Counties	Percent
Below Average	176	50.0%
Above Average	176	50.0%

# Use tabyl to count the counties per multi category level
chr_2022 |> tabyl(median_income_cat) |>
  adorn_pct_formatting(digits = 1) |>
  kbl(col.names = c('Median Income Category', '# of Counties', 'Percent'), 
      align = 'lcc') |>
  kable_classic(full_width = FALSE)

Median Income Category	# of Counties	Percent
Low	119	33.8%
Average	117	33.2%
High	116	33.0%

Our Analytic Tibble

Printing My Tibble

Below is my final tibble containing 352 counties and 11 variables.

chr_2022

# A tibble: 352 × 11
   fipscode state county years…¹ food_…² insuf…³ hs_co…⁴ media…⁵ hs_co…⁶ media…⁷
   <chr>    <fct> <chr>    <dbl>   <dbl>   <dbl>   <dbl>   <dbl> <fct>   <fct>  
 1 12001    FL    Alach…    360.    13.4    36.0    92.8    52.0 Above … Average
 2 12003    FL    Baker…    490.    12.2    43.2    84.9    61.5 Below … High   
 3 12005    FL    Bay C…    479.    15      39.8    90.9    61.3 Above … High   
 4 12007    FL    Bradf…    503.    16.4    41.4    78.9    48.3 Below … Low    
 5 12009    FL    Breva…    418.    12      40.7    92.2    65.9 Above … High   
 6 12011    FL    Browa…    306.     9.9    41.3    89.4    63.9 Above … High   
 7 12013    FL    Calho…    508.    14.7    41.0    77.9    44.0 Below … Low    
 8 12015    FL    Charl…    352.    13.5    39.8    90.8    58.4 Above … Average
 9 12017    FL    Citru…    543.    15.5    42.9    89.5    48.6 Above … Low    
10 12019    FL    Clay …    376.    10.8    41.0    92.1    72.5 Above … High   
# … with 342 more rows, 1 more variable: county_ranked <dbl>, and abbreviated
#   variable names ¹years_lost, ²food_insecurity, ³insufficient_sleep,
#   ⁴hs_completion_raw, ⁵median_income_raw, ⁶hs_completion_cat,
#   ⁷median_income_cat

Summarizing My Tibble

Below is a summary of my final tibble, containing 352 counties and 11 variables, which confirms that I have no missing variables and a sufficient number of distinct raw values. Additional information about these variables, whose names will not change during the course of this project, can be found in the code book.

Hmisc::describe(chr_2022, descript = 'Summary of chr_2022')

Summary of chr_2022 

 11  Variables      352  Observations
--------------------------------------------------------------------------------
fipscode 
       n  missing distinct 
     352        0      352 

lowest : 12001 12003 12005 12007 12009, highest: 47181 47183 47185 47187 47189
--------------------------------------------------------------------------------
state 
       n  missing distinct 
     352        0        4 
                              
Value        OH   IL   FL   TN
Frequency    88  102   67   95
Proportion 0.25 0.29 0.19 0.27
--------------------------------------------------------------------------------
county 
       n  missing distinct 
     352        0      262 

lowest : Adams County     Alachua County   Alexander County Allen County     Anderson County 
highest: Wilson County    Winnebago County Wood County      Woodford County  Wyandot County  
--------------------------------------------------------------------------------
years_lost 
       n  missing distinct     Info     Mean      Gmd      .05      .10 
     352        0      352        1    447.6    115.8    284.7    317.3 
     .25      .50      .75      .90      .95 
   376.4    436.7    515.6    579.8    624.3 

lowest :  215.1964  223.2349  226.0207  235.5931  235.8080
highest:  678.3199  679.4405  681.1674  706.2588 1007.1342
--------------------------------------------------------------------------------
food_insecurity 
       n  missing distinct     Info     Mean      Gmd      .05      .10 
     352        0      113        1    13.23    3.259     8.70     9.90 
     .25      .50      .75      .90      .95 
   11.28    13.00    15.20    17.00    18.00 

lowest :  4.2  5.6  6.1  6.3  6.5, highest: 19.2 19.6 19.7 20.5 21.8
--------------------------------------------------------------------------------
insufficient_sleep 
       n  missing distinct     Info     Mean      Gmd      .05      .10 
     352        0      352        1    39.11    3.726    33.92    34.55 
     .25      .50      .75      .90      .95 
   36.09    39.67    41.60    42.77    43.37 

lowest : 30.64410 32.11241 32.14448 32.20530 32.29310
highest: 45.84424 45.85811 46.02228 46.31325 47.38216
--------------------------------------------------------------------------------
hs_completion_raw 
       n  missing distinct     Info     Mean      Gmd      .05      .10 
     352        0      352        1    87.69    5.435    78.93    80.78 
     .25      .50      .75      .90      .95 
   84.95    88.79    91.52    92.99    93.70 

lowest : 56.14279 69.08033 71.91955 73.15868 73.53464
highest: 95.22472 95.24634 95.81135 96.23150 96.81737
--------------------------------------------------------------------------------
median_income_raw 
       n  missing distinct     Info     Mean      Gmd      .05      .10 
     352        0      351        1    57.11    13.02    42.10    44.30 
     .25      .50      .75      .90      .95 
   48.31    55.00    63.92    71.67    76.34 

lowest :  32.163  33.109  36.527  37.683  38.315
highest:  94.343  97.263 100.325 114.423 118.257
--------------------------------------------------------------------------------
hs_completion_cat 
       n  missing distinct 
     352        0        2 
                                      
Value      Below Average Above Average
Frequency            176           176
Proportion           0.5           0.5
--------------------------------------------------------------------------------
median_income_cat 
       n  missing distinct 
     352        0        3 
                                  
Value          Low Average    High
Frequency      119     117     116
Proportion   0.338   0.332   0.330
--------------------------------------------------------------------------------
county_ranked 
       n  missing distinct     Info     Mean      Gmd 
     352        0        1        0        1        0 
              
Value        1
Frequency  352
Proportion   1
--------------------------------------------------------------------------------

Saving My Tibble

Finally, I saved my tibble as chr_2022_SarahGrabinski.Rds in my project.

saveRDS(chr_2022, file = 'chr_2022_SarahGrabinski.Rds')

Codebook

Table of States with County Counts

I selected states based on whether the state was a toss-up, safely Democrat, or safely Republican based on ratings from Ballotpedia’s compilation of forecasts for the 2020 election to try and balance my sample for policy choices that affect health outcomes. I selected Florida, Illinois, and Tennessee in addition to Ohio because they had a large number of counties each and a similar number of counties to each other, such that no state was unevenly represented in my sample. This selection also had distributions which closely matched the nationwide distribution for most variables, which improves the internal and external validity of my models.

State	Postal Abbreviation	Political Leaning
Ohio	OH	Lean Republican
Florida	FL	Toss Up
Tennessee	TN	Safely Republican
Illinois	IL	Safely Democrat

# Use tabyl to summarize counties by state
chr_2022 |>
  tabyl(state) |>
  adorn_totals() |>
  adorn_pct_formatting() |>
  kbl(col.names = c('State', 'Number of Counties', 'Percent'), 
      align = 'ccc') |>
  kable_classic(full_width = FALSE, 'striped')

State	Number of Counties	Percent
OH	88	25.0%
IL	102	29.0%
FL	67	19.0%
TN	95	27.0%
Total	352	100.0%

Table of Variables, Descriptions and Roles

Variable	v Code	Description	Analytic Role
fipscode	–	5-digit state+county identifier	ID
county	–	name of county	–
state	–	postal abbreviation of state	–
years_lost	v127	years of potential life lost (YPLL) before age 75 per 100k population per year (age-adjusted)	outcome
food_insecurity	v139	% of population who lack adequate access to food	quantitative predictor
insufficient_sleep	v143	% of adults reporting fewer than 7 hrs of sleep on average (age-adjusted)	quantitative predictor
hs_completion_raw	v168	% of adults 25+ with high school diploma or equivalent	–
hs_completion_cat	v168	Above Average (>= 88.8%), Below Average (< 88.8%)*	binary predictor
median_income_raw	v063	median household income in thousands of dollars	–
median_income_cat	v063	Low (< 50.4), Average (50.4-60.8), High (> 60.8), in thousands of dollars**	multi-categorical predictor
county_ranked	–	whether the county is ranked	–

*Median high school completion percentage for all US counties

**Based on 3 tertiles of median income across all US counties

Details on my Variables from CHR

Additional details on my chosen variables can be found via the summaries linked on the County Health Rankings site.

Outcome variable: years_lost was originally v127_rawvalue and is listed in the Length of Life subcategory under Health Outcomes at County Health Rankings. It is a rate which quantifies the number of years of potential life lost (YPLL) before age 75 per 100,000 people per year. It is based on the sum of all years lost before age 75 from 2018-2020 according to the National Center for Health Statistics Mortality Files divided by the total population of the county during that time, and it was age-adjusted using the 2000 census data.
Quantitative Predictor 1: food_insecurity was originally v139_rawvalue and is listed in the Diet and Exercise subcategory of the Health Behaviors category under Health Factors at County Health Rankings. It estimates the proportion of county residents who lack adequate access to food, including the ability to provide balanced meals, as determined by Map The Meal Gap project. It was multiplied by 100 to convert it from a proportion to a percentage. Data from 2019 was used in the Core Food Insecurity Model, which pulls information from the Community Population Survey, Bureau of Labor Statistics, and American Community Survey.
Quantitative Predictor 2: insufficient_sleep was originally v143_rawvalue and is listed in the Other Health Behaviors subcategory of the Health Behaviors category under Health Factors at County Health Rankings. It estimates the proportion of county residents who report sleeping less than 7 hours per night on average. It was multiplied by 100 to convert it from a proportion to a percentage. It is calculated using 2018 Behavioral Risk Factor Surveillance System survey results and modeled by the PLACES project using data for the American Community Survey. It is age-adjusting using the 2000 census data.
Binary Predictor: hs_completion_raw was originally v168_raw_value and is listed in the Education subcategory of the Social & Economic Factors category under Health Factors at County Health Rankings. This measure is the proportion of adults ages 25+ with a high school diploma or equivalent and is calculated from 2016-2020 American Community Survey data. It was multiplied by 100 to convert it from a proportion to a percentage and split into two categories to become hs_completion_cat. The raw value was split into ‘Above Average’ and ‘Below Average’ categories using the median high school completion percentage for all US counties, 88.8%.
Multi-Categorical Predictor: median_income_raw was originally v063_raw_value. This measure is the median household income, or the income where half of households in a county earn more and half of households earn less. It is based on 2020 data and modeling from the US Census Bureau using American Community Survey data. It was divided by 1000 to represent income in thousands of dollars and was split into three categories to become median_income_cat. The raw value was split into three tertiles using the distribution of median household incomes across all US counties. ‘Low’ median household incomes are less than $50,397, ‘Average’ median household incomes range from $50,398 to $60,754, and ‘High’ median household incomes are greater than $60,755.

Biggest Challenge

The most challenging part of my proposal was organization. I was having difficulty ensuring I completed all tasks when following the sample proposal. To me, and probably by design, it seemed less like a template and more like a road map. I also wanted my proposal to appear like a report so I could potentially add it to my portfolio. I finished variable selection and the coding portion of the proposal prior to the early submission deadline. I found myself spending a great deal of subsequent time trying to scroll back and forth to make sure I had completed all the tasks in various locations. Eventually, your advice to not spend more than 15’ on a problem kicked in. I stopped working and took a step back. I ignored all my code and created an outline of my proposal based only on the requirements. Once I was satisfied with the order, it took me very little time compared to how much I would have spent with my previous strategy to complete and check my work. My biggest concern remaining was that by deviating from the sample proposal, I made the requirements too difficult to find, even though it made more sense to me arranged like this.

For this final project, I rearranged everything to match the sample.

Analysis 1

The Variables

The predictive variable I chose for this analysis is the percentage of residents experiencing food insecurity (food_insecurity), which estimates the proportion of residents in each county who lack adequate access to food or the ability to provide balanced meals. The outcome I will predict is the rate of premature mortality (years_lost) in years of potential life lost before the age of 75 per 100,000 people per year (YPLL). Neither food_insecurity nor years_lost is missing data for any of the 352 counties in Ohio, Florida, Illinois, and Tennessee. Although no data is missing, I will use a tibble called model1_data that contains only fipscode, state, county, years_lost, and food_insecurity for simplicity’s sake.

In Cuyahoga County, Ohio, the rate of premature mortality is 431.16 years of potential life lost before age 75 per 100,000 people per year, and the CHR estimates that 13.9% of residents experience food insecurity.

# Create a limited data set for model 1
model1_data <- chr_2022 |>
  select(fipscode, state, county, years_lost, food_insecurity)

# Identify and display the values for Cuyahoga County
model1_data |>
  filter(state == 'OH', county == 'Cuyahoga County') |>
  select(state, county, years_lost, food_insecurity) |>
  kbl(col.names = c('State', 'County', 'years_lost', 'food_insecurity'), 
      align = 'llcc', digits = 2) |>
  kable_classic(full_width = FALSE)

State	County	years_lost	food_insecurity
OH	Cuyahoga County	431.16	13.9

Research Question

Since lack of consistent access to food is linked to negative health outcomes, as the percentage of residents experiencing food insecurity increases in 352 counties in Ohio, Illinois, Tennessee, and Florida, at what rate does the county’s risk of premature mortality, as assessed by years of potential life lost before the age of 75 per 100,000 people per year, also increase?

Data Visualization

There is a positive relationship between the percentage of county residents experiencing food insecurity (predictor) and the years of potential life lost before age 75 (YPLL) per 100,000 people per year (outcome), such that as the prevalence of food insecurity increases by 1%, the risk of premature mortality increases by approximately 75 YPLL per 100,000 people per year. There is not an obvious pattern with regards to the state in which a county resides. A linear model is appropriate here as the LOESS curve closely approximates the linear fitted line. The points are also closely clustered along the length of both models. There is one significant outlier (Union County, Florida), which is about 300 YPLL above the next highest value.

ggplot(model1_data, aes(x = food_insecurity, y = years_lost)) +
  geom_point(aes(color = state), alpha = 0.5) +
  scale_color_viridis_d(name = 'State') + 
  geom_smooth(method = 'lm', formula = y ~ x, se = FALSE, col = 'red') +
  geom_smooth(method = 'loess', formula = y ~ x, se = FALSE, col = 'blue') +
  geom_label_repel(data = filter(model1_data, years_lost > 1000),
             aes(x = food_insecurity, y = years_lost,
                 label = paste(county, state, sep = ', '))) +
  labs(x = '% of County Residents Experiencing Food Insecurity', 
       y = 'YPLL Per 100,000 People Per Year', 
       title = 
         'Predicting Premature Mortality Rate by Food Insecurity Prevalence',
       subtitle = paste("Pearson r = ", 
                         round_half_up(cor(model1_data$food_insecurity, 
                                           model1_data$years_lost),
                                       3)),
       caption = 'YPLL = years of potential life lost before age 75') +
  theme(legend.position = c(0.1, 0.7),
        legend.background = element_rect(fill = "white", color = "black"))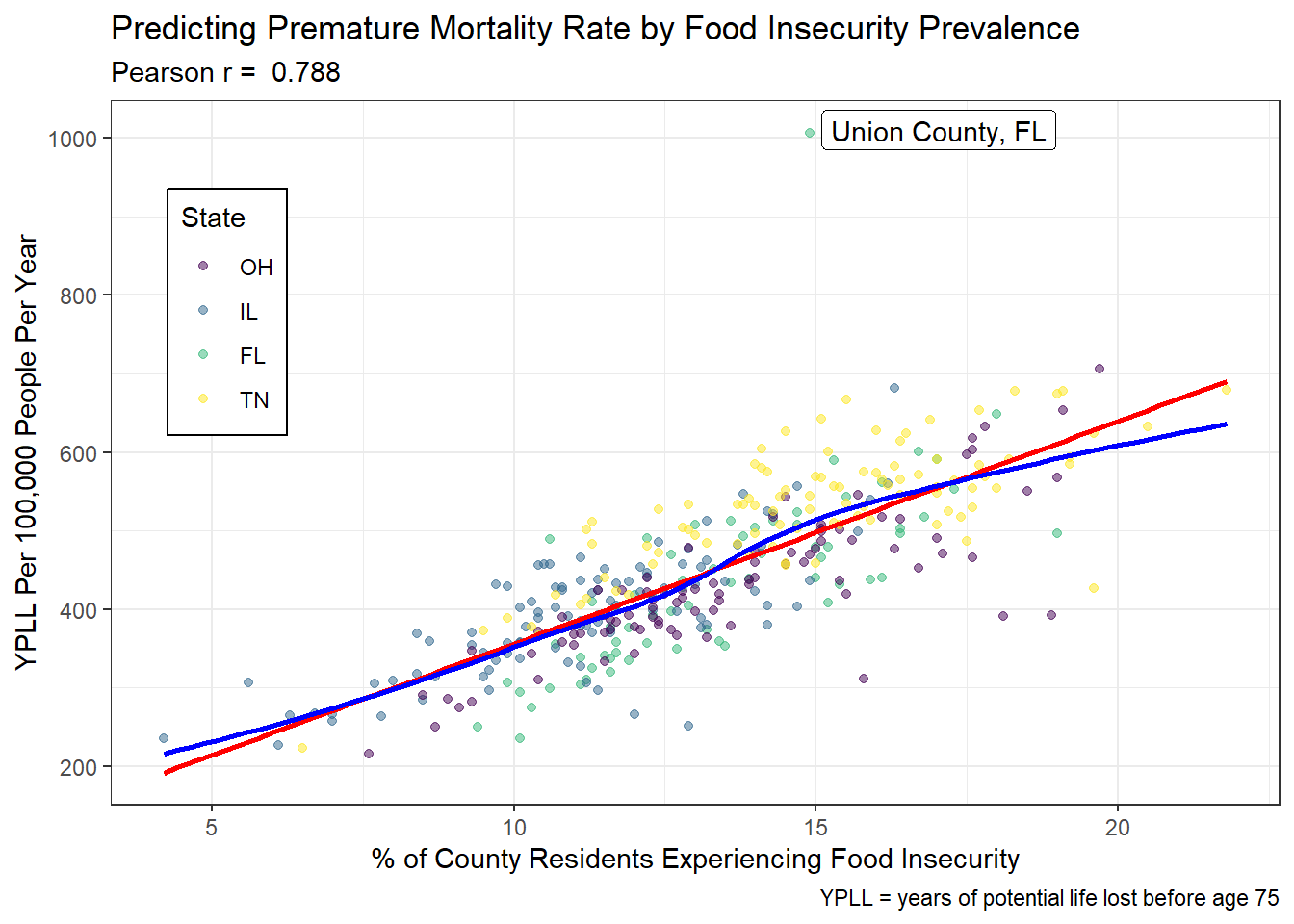

Transformation Assessment

The most promising transformation was the log of YPLL. A Box-Cox plot for my 3 predictors (food_insecurity, median_income_cat, insufficient_sleep) versus my outcome (years_lost) recommended a power transformation of approximately lambda = 0.5, which is the square root and not an available option. The estimate of lambda ranged from 0 to 1, indicating the next best options were to use a log transformation or to not transform at all. As seen below, the loess curve tracks the linear curve for the transformed data, although less well than for the untransformed data. Using this transformation also did not violate any of the assumptions about the residuals of linear models. I decided not to use a transformation of my outcome because without noticeable cost to fit, using the untransformed data produces a more easily interpreted model for my audience. Communication is a key component of the ‘Conclusion’ step of the PPDAC cycle, so I have prioritized simplicity at little cost to the model for the sake of my audience’s understanding.

ggplot(model1_data, aes(x = food_insecurity, y = log(years_lost))) +
  geom_point(aes(color = state), alpha = 0.5) +
  geom_smooth(formula = y ~ x, method = 'lm', se = FALSE, col = 'red') +
  geom_smooth(formula = y ~ x, method = 'loess', se = FALSE, col = 'blue') +
  geom_label_repel(data = filter(model1_data, years_lost > 1000),
             aes(x = food_insecurity, y = log(years_lost),
                 label = paste(county, state, sep = ', '))) +
  scale_color_viridis_d(name = 'State') + 
  labs(x = '% of County Residents Experiencing Food Insecurity', 
       y = 'Natural Log of YPLL Per 100,000 People Per Year', 
       title = 
         'Predicting Premature Mortality Rate by Food Insecurity Prevalence',
       subtitle = paste("Pearson r = ", 
                         round_half_up(cor(model1_data$food_insecurity, 
                                           log(model1_data$years_lost)),
                                       3)),
       caption = 'YPLL = years of potential life lost before age 75') +
  theme(legend.position = c(0.1, 0.7),
        legend.background = element_rect(fill = "white", color = "black"))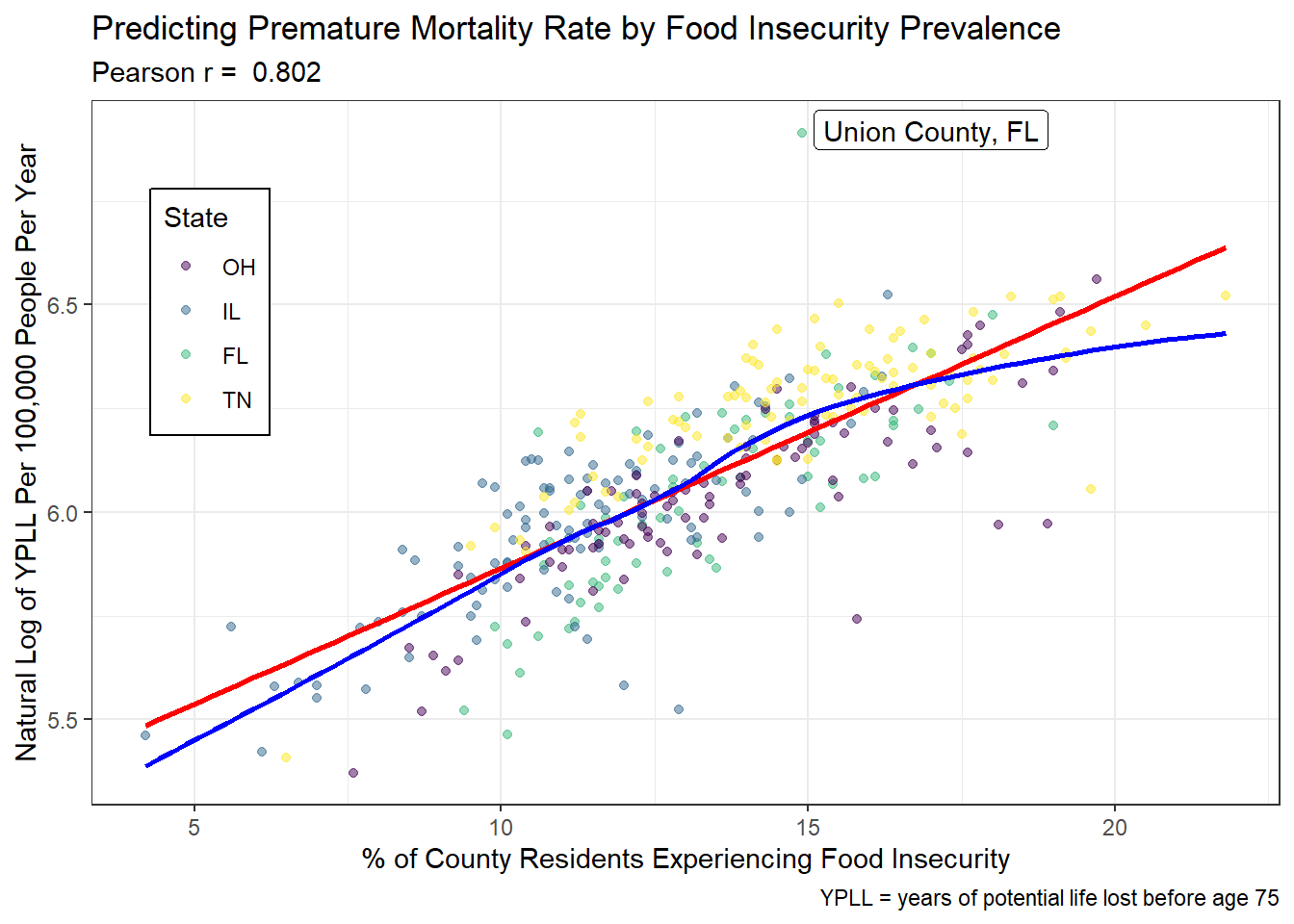

The Fitted Model

The Prediction Equation

This linear model predicts that the years of potential life lost before age 75 per 100,000 people per year is 72.51 YPLL (y-intercept) plus 28.35 times the percentage of county residents experiencing food insecurity.

# Create the linear model
model1 <- lm(years_lost ~ food_insecurity, data = model1_data)

# Extract the equation
extract_eq(model1, use_coefs = TRUE, coef_digits = 2)

\[ \operatorname{\widehat{years\_lost}} = 72.51 + 28.35(\operatorname{food\_insecurity}) \]

The Model Coefficients

The y-intercept for this model is 72.51 YPLL (90% CI: 46.09-98.92) with a standard error of 16.02 YPLL and the slope is 28.35 YPLL per percent of residents experiencing food insecurity (90% CI: 26.40-30.30) with a standard error of 1.18 YPLL per percent of residents experiencing food insecurity.

# Use tidy to extract the estimates, SE, and a 90% CI for model coefficients
tidy(model1, conf.int = TRUE, conf.level = 0.9) |>
  select(term, estimate, std.error, conf.low, conf.high) |>
  kbl(col.names = c('Term', 'Estimate', 'Std. Error', 
                    '90% CI Low', '90% CI High'), 
      digits = 2, align = 'lcccc', 
      caption = 'Model Coefficients') |>
  kable_classic(full_width = FALSE)

Model Coefficients
Term	Estimate	Std. Error	90% CI Low	90% CI High
(Intercept)	72.51	16.02	46.09	98.92
food_insecurity	28.35	1.18	26.40	30.30

Summaries of Model Fit

The correlation between food insecurity and premature mortality rate is 0.788. Using 352 counties to predict YPLL by the prevalence of food insecurity, the variance in food insecurity explains 62.1% (R² = 0.621) of the variation in premature mortality rate. The residual standard error of this model is 63.95 years of potential life lost before age 75 per 100,000 people per year.

# Use glance to extract R2, RSE, and # of counties from model1
glance(model1) |>
  select(r.squared, sigma, nobs) |>
  # Take the square root of R-squared to calculate Pearson's r
  mutate(correlation = sqrt(r.squared)) |>
  kbl(col.names = c('R-Squared', 'Residual Std Error', 
                    '# of Counties', 'Correlation'), 
      digits = c(3, 2, 0, 3), align = 'c', 
      caption = 'Model Fit Summaries') |>
  kable_classic(full_width = FALSE)

Model Fit Summaries
R-Squared	Residual Std Error	# of Counties	Correlation
0.621	63.95	352	0.788

Residual Analysis

This model conforms to all the assumptions of a linear model. The regression relationship is linear as no curve forms when plotting the residuals against the fitted values. Although there are a few outliers not well predicted by the model, the regression residuals overall show similar variance across all levels of the fitted values with no meaningful pattern. Finally, minus a few outliers at the extremes, the residuals are well described by a normal model as demonstrated by the Q-Q plot.

# Augment model1 with the original data
model1_aug <- augment(model1, data = model1_data)

p1 <- ggplot(model1_aug, aes(x = .fitted, y = .resid)) +
  geom_point(color = 'lightslategrey', alpha = 0.5) +
  geom_smooth(method = 'lm', formula = y ~ x, se = FALSE, col = 'red') +
  geom_smooth(method = 'loess', formula = y ~ x, se = FALSE, col = 'blue') +
  labs(x = 'Fitted Values of YPLL', 
       y = 'Residual Values of YPLL', 
       title = 'Residual vs Fitted Values of YPLL',
       caption = 'YPLL = years of potential life lost before age 75')

p2 <- ggplot(model1_aug, aes(sample = .resid)) +
  geom_qq(color = 'lightslategrey', alpha = 0.5) +
  geom_qq_line() +
  labs(x = 'Expected Quantile', 
       y = 'Actual Value', 
       title = 'Q-Q Plot')

p1 + p2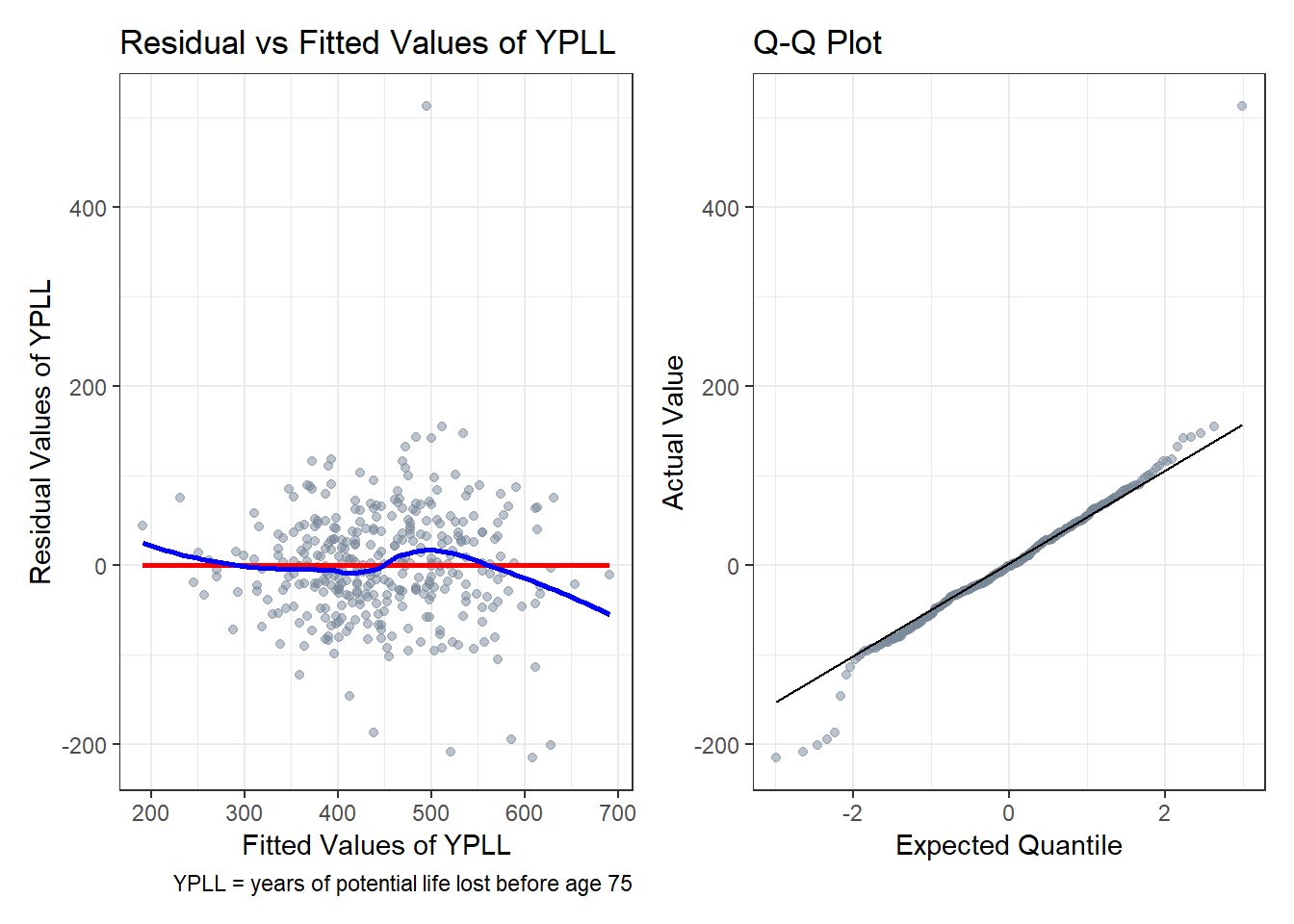

For Cuyahoga County, Ohio, the fitted model value of 466.58 YPLL reasonably approximates the actual value of 431.16 YPLL with a residual of -35.41 YPLL.

# Select and display Cuyahoga County's stats from the augmented model
model1_aug |>
  filter(state == 'OH', county == 'Cuyahoga County') |>
  select(state, county, years_lost, .fitted, .resid) |>
  kbl(col.names = c('State', 'County', 'Actual', 'Fitted', 'Residual'), 
      digits = 2, align = 'llccc', 
      caption = 
        'Cuyahoga County, OH - Years of Premature Life Lost') |>
  kable_classic(full_width = FALSE)

Cuyahoga County, OH - Years of Premature Life Lost
State	County	Actual	Fitted	Residual
OH	Cuyahoga County	431.16	466.58	-35.42

Unsurprisingly, the county predicted least well by this model is Union County, Florida with a residual of 512.20 YPLL. The second worst prediction by this model is for Athens County, Ohio with a residual of -215.81 YPLL.

# Select and display the 2 counties with the worst residuals
model1_aug |>
  arrange(desc(abs(.resid))) |>
  select(state, county, years_lost, .fitted, .resid) |>
  head(2) |>
  kbl(col.names = c('State', 'County', 'Actual', 'Fitted', 'Residual'), 
      digits = 2, align = 'llccc', 
      caption = 
        'Least Successfully Fitted Counties') |>
  kable_classic(full_width = FALSE)

Least Successfully Fitted Counties
State	County	Actual	Fitted	Residual
FL	Union County	1007.13	494.93	512.20
OH	Athens County	392.53	608.34	-215.81

Conclusions and Limitations

It has been demonstrated that the lack of consistent access to food is associated with negative health outcomes, so this model sought to determine the degree to which premature mortality risk increases, as measured by years of potential life lost before age 75 per 100,000 people per year, with each increase in the percentage of county residents who experience food insecurity. This model indicates a positive relationship between the two measures and predicts that with a 1% increase in the prevalence of food insecurity in a county, the premature mortality rate will increase by 26.40-30.30 YPLL per 100,000 people per year. Using a risk ratio calculation, this amounts to a 4-15% increase in risk with every 1% increse in food insecurity prevalence. The y-intercept is non-negative (90% CI: 46.09-98.92), which suggests that eliminating food insecurity would not eliminate the risk of premature mortality.

A key limitation of this model is that the prevalence of food insecurity in a county is a modeled value based on survey responses, poverty, unemployment, home ownership, and disability prevalence measures at the state level. Self-reported data may not accurately represent the true nature of my sample, and the assumptions that produce this model may not hold for counties with small populations, which both limit the inferences which can be drawn about the sample from this data. In fact, of the top 10 worst predicted counties, Athens County is the only county with a population greater than 20,000. My sample is not truly random, which threatens internal validity, although the distribution of food insecurity prevalence does match the nationwide distribution. Additionally, poverty is used to estimate food insecurity in the original model. Poverty is strongly associated with premature mortality, so this relationship may indicate a confounding variable rather than a true association.

Analysis 2

The Variables

The predictive variable I chose for this analysis is the median household income (median_income_cat), divided into ‘Low’, ‘Average’, and ‘High’ tertiles, which estimates the median household income of residents in each county. The outcome I will predict is the rate of premature mortality (years_lost) in years of potential life lost (YPLL) before the age of 75 per 100,000 people per year. Neither median_income_cat nor years_lost is missing data for any of the 352 counties in Ohio, Florida, Illinois, and Tennessee. Although no data is missing, I will use a tibble called model2_data that contains only fipscode, state, county, years_lost, and median_income_cat for simplicity’s sake. In Cuyahoga County, Ohio, the rate of premature mortality is 431.16 years lost per 100,000 people per year, and the median household income is $55,128.

# Create a limited data set for model 2
model2_data <- chr_2022 |>
  select(fipscode, state, county, years_lost, 
         median_income_cat, median_income_raw)

# Identify and display the values for Cuyahoga County
model2_data |>
  filter(state == 'OH', county == 'Cuyahoga County') |>
  select(state, county, years_lost, median_income_raw, median_income_cat) |>
  kbl(col.names = c('State', 'County', 'years_lost', 
                    'Raw Median Income', 'Income Category'), 
      align = 'llccc', digits = 2) |>
  kable_classic(full_width = FALSE)

State	County	years_lost	Raw Median Income	Income Category
OH	Cuyahoga County	431.16	55.13	Average

Research Question

Knowing poverty’s negative impact on health outcomes, among 352 counties in Ohio, Illinois, Florida, and Tennessee, do counties with lower median household incomes disproportionately bear the costs of premature mortality, as measured by years of premature life lost before age 75 per 100,000 people per year, or does this effect persist in counties with average median incomes as well?

Data Visualization

There is a negative relationship between the median household income (predictor) and the years of potential life lost before age 75 (YPLL) per 100,000 people per year (outcome), such that as the median household income increases, the risk of premature mortality decreases. There is a great deal of overlap, so the observed differences may not be meaningful. Values are approximately normally distributed within each category, and the categories appear to have similar variances, therefore using a linear model would be appropriate. There is one significant outlier (Union County, Florida), which is about 300 YPLL above the next highest value.

ggplot(model2_data, aes(x = years_lost, y = median_income_cat)) +
  geom_violin(aes(fill = median_income_cat), alpha = 0.5) +
  geom_boxplot(width = 0.3, notch = TRUE) +
  stat_summary(fun = "mean", geom = "point", 
               shape = 23, size = 3, fill = "white") +
  scale_fill_viridis_d(name = 'Median Income') +
  geom_label_repel(data = filter(model2_data, years_lost > 1000),
             aes(x = years_lost, y = median_income_cat,
                 label = paste(county, state, sep = ', ')), nudge_y = 0.25) +
  labs(x = 'YPLL per 100,000 people per year', 
       y = 'Median Household Income', 
       title = 'Premature Mortality Rates by Median Household Income',
       caption = 'YPLL = years of potential life lost before age 75') +
  guides(fill = 'none')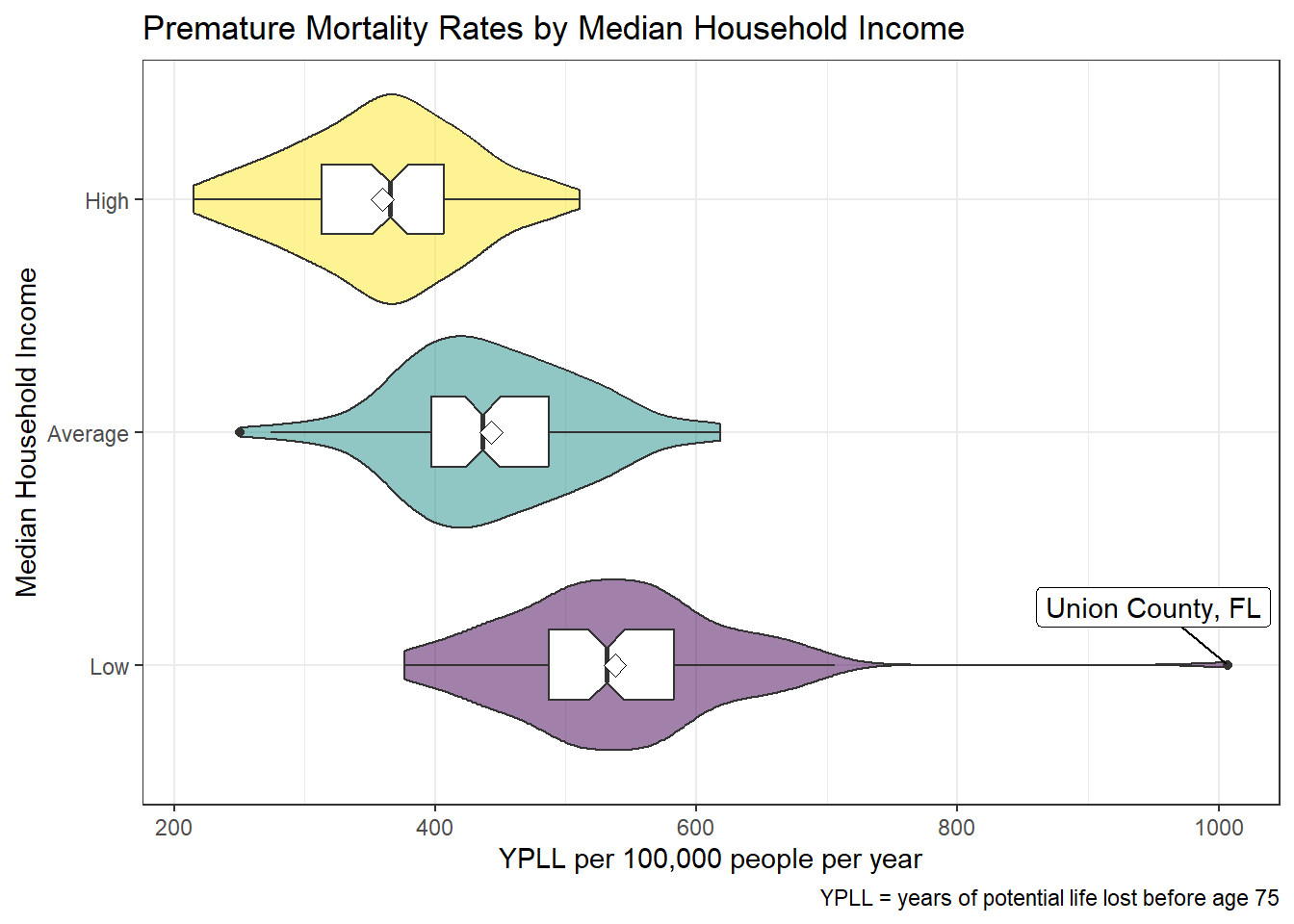

The Fitted Model

The Prediction Equation

After fitting a linear model, the years of potential life lost before age 75 per 100,000 people per year is predicted to be 537.69 YPLL for counties with a low median income, 94.72 years lower than the low median income or 442.97 YPLL for counties with average median incomes, and 177.93 years lower than the low median income or 359.76 YPLL for counties with high median incomes.

# Create the linear model
model2 <- lm(years_lost ~ median_income_cat, data = model2_data)

# Extract the equation
extract_eq(model2, use_coefs = TRUE, wrap = TRUE, 
           terms_per_line = 1, coef_digits = 2, operator_location = 'start',
           swap_var_names = c('median_income_cat' = 'median_income'))

\[ \begin{aligned} \operatorname{\widehat{years\_lost}} &= 537.69\\ &\quad - 94.72(\operatorname{median\_income}_{\operatorname{Average}})\\ &\quad - 177.93(\operatorname{median\_income}_{\operatorname{High}}) \end{aligned} \]

The Model Coefficients

The intercept, representing YPLL for low median incomes, is predicted to be 537.69 (90% CI: 526.48-548.89). The coefficient for the average median income category is predicted to be 94.72 YPLL lower than that for low median incomes, resulting in a predicted value of 442.97 YPLL (90% CI: 426.82-458.88). The coefficient for the high median income category is predicted to be 177.93 YPLL lower than that for low median incomes, resulting in a predicted value of 359.76 YPLL (90% CI: 343.82-375.71).

# Use tidy to extract the term, estimate, std error, and 90% CI from model2
tidy(model2, conf.int = TRUE, conf.level = 0.9) |>
  select(term, estimate, std.error, conf.low, conf.high) |>
  kbl(col.names = c('Term', 'Estimate', 'Std. Error', 
                    '90% CI Low', '90% CI High'), 
      digits = 2, align = 'lcccc', 
      caption = 'Model Coefficients') |>
  kable_classic(full_width = FALSE)

Model Coefficients
Term	Estimate	Std. Error	90% CI Low	90% CI High
(Intercept)	537.69	6.79	526.48	548.89
median_income_catAverage	-94.72	9.65	-110.63	-78.81
median_income_catHigh	-177.93	9.67	-193.87	-161.98

Summaries of Model Fit

The correlation between the median income category and premature mortality rate is 0.702. Using 352 counties to predict YPLL by whether the county has a low, average, or high median household income, median income explains 49.3% (R² = 0.493) of the variation in premature mortality rate. The residual standard error of this model is 74.1 years of potential life lost before age 75 per 100,000 people per year.

# Use glance to select the R-squared, residual SE, and # of counties
glance(model2) |>
  select(r.squared, sigma, nobs) |>
  # Take the square root of R-squared to calculate Pearson's r
  mutate(correlation = sqrt(r.squared)) |>
  kbl(col.names = c('R-Squared', 'Residual Std Error', 
                    '# of Counties', 'Correlation'), 
      digits = c(3, 2, 0, 3), align = 'c', 
      caption = 'Model Fit Summaries') |>
  kable_classic(full_width = FALSE)

Model Fit Summaries
R-Squared	Residual Std Error	# of Counties	Correlation
0.493	74.1	352	0.702

Prediction Analysis

Residual Plot

This model conforms to all the assumptions of a linear model. Linearity is not relevant for a categorical model, but besides Florida’s outlying county, the residuals show similar variance across all levels of the fitted values with no meaningful pattern. Finally, minus the outlier, the residuals are well described by a normal model across all levels as demonstrated by the Q-Q plot.

# Augment model2 with the original data
model2_aug <- augment(model2, data = model2_data)

# Set seed to prevent the jitter from moving
set.seed(4212022)

p1 <- ggplot(model2_aug, aes(x = jitter(.fitted), y = .resid)) +
  geom_boxplot(aes(group = median_income_cat), width = 10, 
               outlier.shape = NA) + 
  geom_point(aes(col = median_income_cat), alpha = 0.25) +
  scale_color_viridis_d(name = 'Median Income') +
  geom_label_repel(data = filter(model2_aug, years_lost > 1000),
                   aes(x = jitter(.fitted), y = .resid, 
                       label = paste(county, state, sep = ', ')), 
                   nudge_x = -6, min.segment.length = 1) +
  labs(x = 'Fitted Values', 
       y = 'Residual Values', 
       title = 'Fitted vs Residual Values',
       subtitle = 'by Median Income') +
  guides(color = 'none')

p2 <- ggplot(model2_aug, aes(sample = .resid)) +
  geom_qq(aes(color = median_income_cat), alpha = 0.25) +
  geom_qq_line() +
  scale_colour_viridis_d() +
  facet_wrap(~ median_income_cat, ncol = 1) +
  labs(x = 'Expected Quantile', 
       y = 'Actual Value', 
       title = 'Q-Q Plot by Median Income') +
  guides(color = 'none')

p1 + p2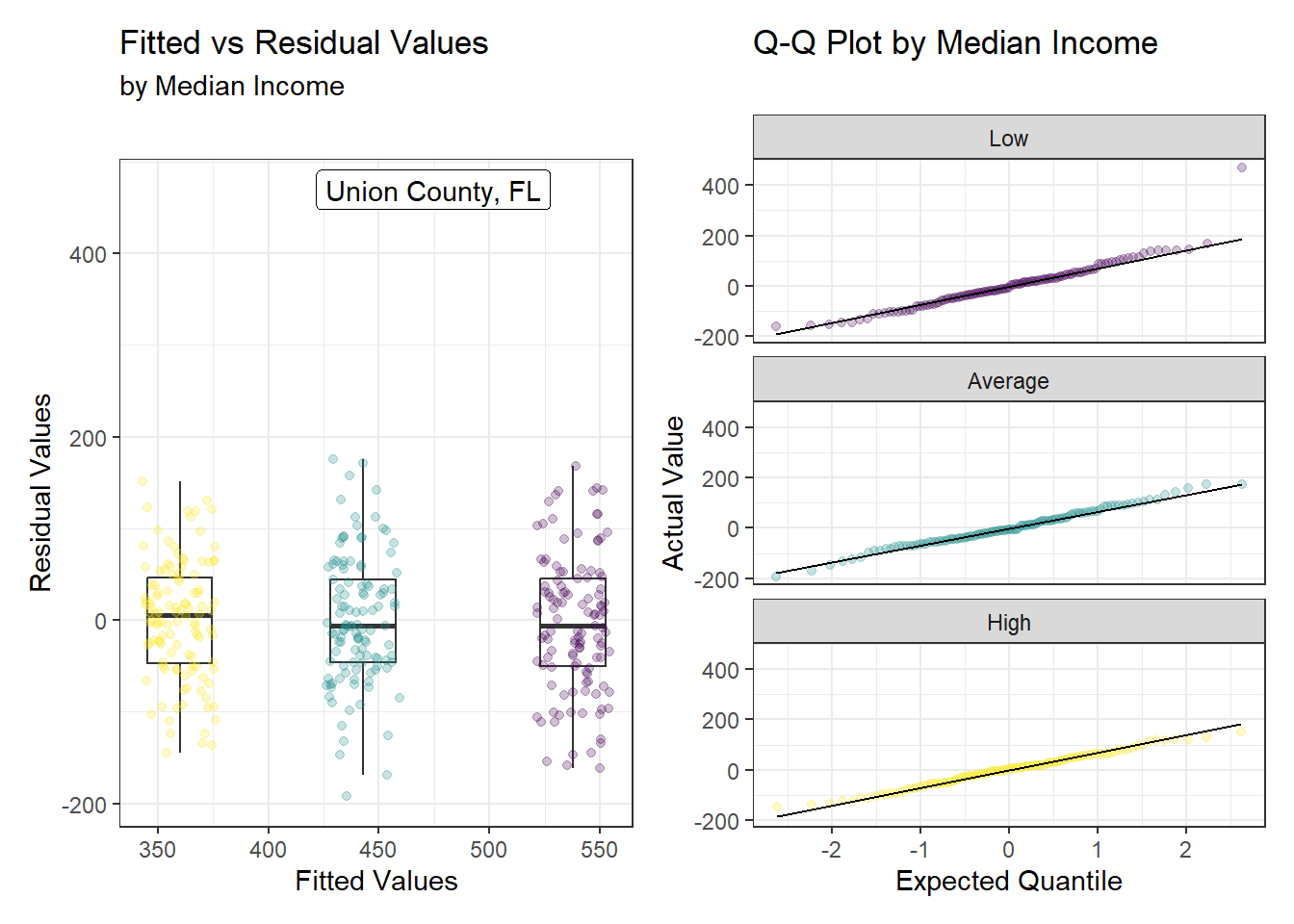

Prediction for Cuyahoga County, OH

For Cuyahoga County, Ohio, which has an average median household income, the fitted model value of 442.96 approximates well the actual value of 431.16 YPLL with a residual of -11.8 YPLL.

# Select and display Cuyahoga County's stats from the augmented model
model2_aug |>
  filter(state == 'OH', county == 'Cuyahoga County') |>
  select(state, county, median_income_cat, years_lost, .fitted, .resid) |>
  kbl(col.names = c('State', 'County', 'Income Category', 
                    'Actual', 'Fitted', 'Residual'), 
      digits = 2, align = 'llcccc', 
      caption = 
        'Cuyahoga County, OH - Years of Premature Life Lost') |>
  kable_classic(full_width = FALSE)

Cuyahoga County, OH - Years of Premature Life Lost
State	County	Income Category	Actual	Fitted	Residual
OH	Cuyahoga County	Average	431.16	442.96	-11.8

My Two Least Successfully Fit Counties

Once again, the county predicted least well by this model is Union County, Florida with a residual of 469.45 YPLL. The second worst prediction by this model is for Jasper County, Illinois with a residual of -192.25 YPLL.

# Select and display the 2 counties with the worst residuals
model2_aug |>
  arrange(desc(abs(.resid))) |>
  select(state, county, years_lost, .fitted, .resid) |>
  head(2) |>
  kbl(col.names = c('State', 'County', 'Actual', 'Fitted', 'Residual'), 
      digits = 2, align = 'llccc', 
      caption = 
        'Least Successfully Fitted Counties') |>
  kable_classic(full_width = FALSE)

Least Successfully Fitted Counties
State	County	Actual	Fitted	Residual
FL	Union County	1007.13	537.69	469.45
IL	Jasper County	250.71	442.96	-192.25

Conclusions and Limitations

Given that poverty is known to negatively impact health outcomes, this model sought to determine if counties with lower median household incomes among 352 counties in Ohio, Illinois, Florida, and Tennessee disproportionately bear the costs of premature mortality as compared to those counties with average median incomes and high median incomes. The model predicted 90% confidence intervals for the mean years of potential life lost before age 75 per 100,000 people per year, a measure of risk. Using risk ratio calculations, counties with low median incomes have a 14.7-28.9% increased risk of premature mortality as compared to those with average median incomes, and counties with average median incomes have a 13.6-33.5% increased risk of premature mortality compared to those with high median incomes. These are not meaningfully different levels of risk, so based on this model, counties with low median incomes do not experience disproportionate risk of premature mortality.

As with Analysis 1, a key limitation of this model is that the median household income of a county is a modeled value. The assumptions used in that model may not hold for counties with small populations. Union County, Florida is again the worst fitted county in my model, followed by Jasper County, Illinois with a population of 9,698. Another limitation of this model is that the median income calculation does not include income from capital gains, which are highly concentrated in wealthy counties, or public assistance or welfare payments, which are concentrated in poorer counties. This measure may underestimate the true resources of those at the top and overestimate those of the bottom of the distribution of median incomes, threatening the inferences we can draw about our sample from the data. My sample is also not truly random, which threatens internal validity, although the distribution of incomes does match the nationwide distribution.

Analysis 3

The Variables

The predictive variables for this analysis are the percentage of residents getting insufficient sleep (insufficient_sleep), which estimates the proportion of residents getting less than 7 hours of sleep per night, and the state of the county. The outcome I will predict is the rate of premature mortality (years_lost) in years of potential life lost (YPLL) before the age of 75 per 100,000 people per year. Neither insufficient_sleep, state, nor years_lost is missing data for any of the 352 counties in Ohio, Florida, Illinois, and Tennessee. Although no data is missing, I will use a tibble called model3_data that contains only fipscode, state, county, years_lost, and insufficient_sleep for simplicity’s sake. In Cuyahoga County, Ohio, the rate of premature mortality is 431.16 years lost per 100,000 people per year, and the CHR estimates that 44.85% of residents get less than 7 hours of sleep per night.

# Create a limited data set for model 3
model3_data <- chr_2022 |>
  select(fipscode, state, county, years_lost, insufficient_sleep)

# Identify and display the values for Cuyahoga County
model3_data |>
  filter(state == 'OH', county == 'Cuyahoga County') |>
  select(state, county, years_lost, insufficient_sleep) |>
  kbl(col.names = c('State', 'County', 'years_lost', 'insufficient_sleep'), 
      align = 'llcc', digits = 2) |>
  kable_classic(full_width = FALSE)

State	County	years_lost	insufficient_sleep
OH	Cuyahoga County	431.16	44.85

Research Question

Given the known negative health consequences of the lack of sleep, how many additional years of potential life lost per 100,000 people are attributable to an increase in the prevalence of insufficient sleep amongst residents of 352 counties in Ohio, Illinois, Florida, and Tennessee, and does this relationship differ based on the state in which the county is located?

Data Visualization

When the data is considered in aggregate, there is a positive relationship between the percentage of county residents getting less than 7 hours of sleep per night (predictor) and the years of potential life lost before age 75 (YPLL) per 100,000 people per year (outcome), such that as the percentage of residents getting insufficient sleep increases by 1%, the YPLL increases by 20 years. Illinois counties cluster separately from Ohio, Florida, and Tennessee, and the YPLL and insufficient sleep values for Tennessee counties are higher on average than the other states, so including state as a variable in this model is appropriate. When states are considered individually, the positive relationship holds, but the increase in premature mortality rate per increase in percentage of residents getting insufficient sleep seems to vary slightly, with Tennessee changing the least and Illinois appearing to change the most. A linear model is appropriate here as the LOESS curve closely approximates the linear fitted line for all states, and points are closely clustered along the length of the curves. An interaction term should be use because the slope of the fitted line seems to change by state. There is still one significant outlier, Union County, Florida, which is about 300 YPLL above the next highest value.

p1 <- ggplot(model3_data, aes(x = insufficient_sleep, y = years_lost)) +
  geom_point(aes(color = state), alpha = 0.5) +
  guides(color = 'none') +
  scale_color_viridis_d() +
  geom_smooth(method = 'lm', formula = y ~ x, se = FALSE, col = 'red') +
  geom_smooth(method = 'loess', formula = y ~ x, se = FALSE, col = 'blue') +
  geom_label_repel(data = filter(model3_data, years_lost > 1000),
             aes(x = insufficient_sleep, y = years_lost,
                 label = paste(county, state, sep = ', ')),
             nudge_x = -2) +
  labs(x = '% of residents getting insufficient sleep', 
       y = 'YPLL per 100,000 people per year', 
       title = 'Premature Mortality Rate', 
       subtitle = 'vs Percent Getting Insufficient Sleep', 
       caption = 'YPLL = years of potential life lost before age 75')

p2 <- ggplot(model3_data, aes(x = insufficient_sleep, y = years_lost)) +
  geom_point(aes(color = state), alpha = 0.5) +
  facet_wrap(~state) +
  guides(color = 'none') +
  scale_color_viridis_d() +
  geom_smooth(method = 'lm', formula = y ~ x, se = FALSE, col = 'red') +
  geom_smooth(method = 'loess', formula = y ~ x, se = FALSE, col = 'blue') +
  labs(x = '% of residents getting insufficient sleep', 
       y = 'YPLL per 100,000 people per year', 
       title = 'Premature Mortality Rate', 
       subtitle = 'vs Insufficient Sleep by State', 
       caption = 'Insufficient sleep = less than 7 hours per night')

p1 + p2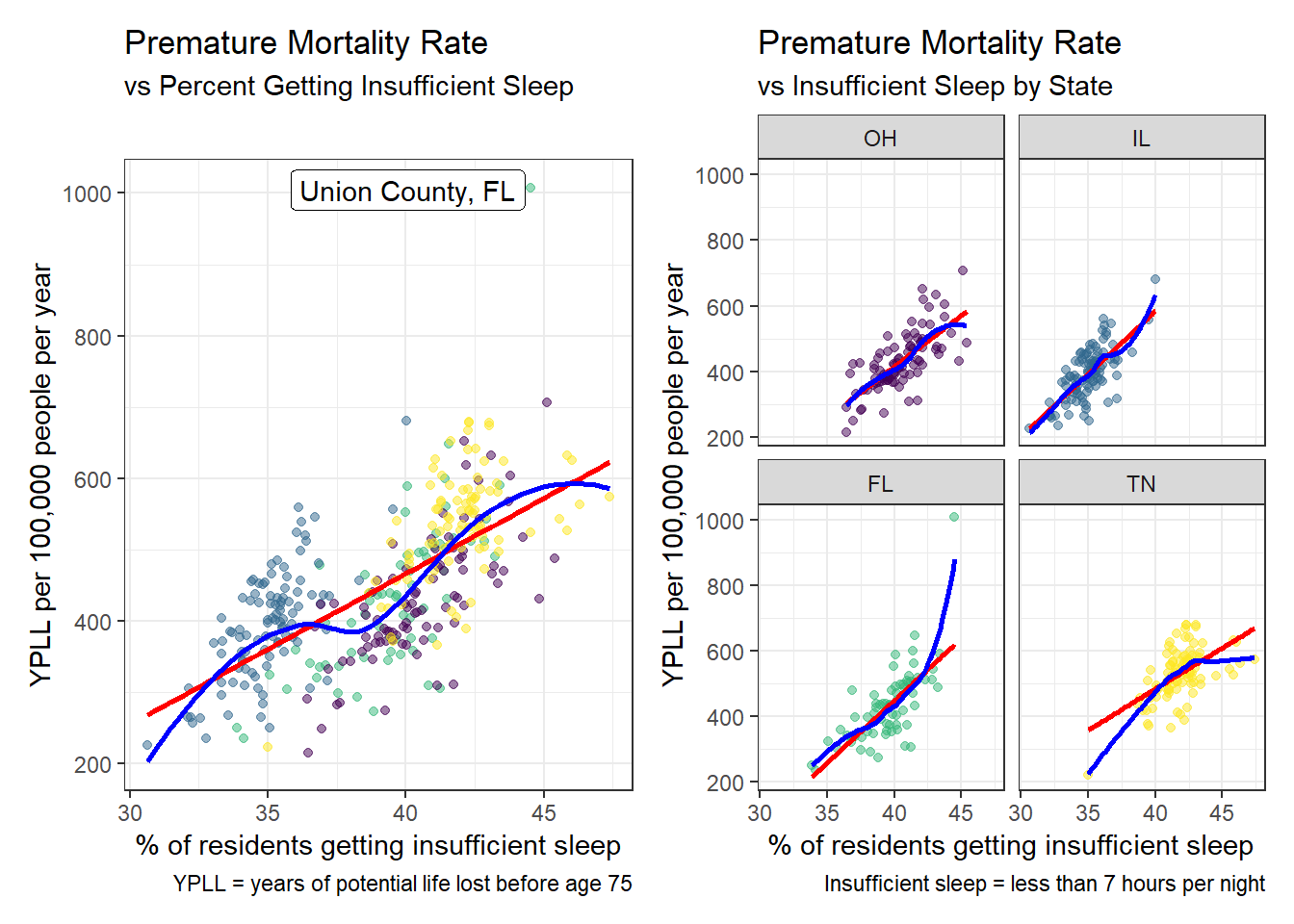

The Fitted Model

The Prediction Equation

The equation for the fitted model is -834.66 YPLL minus 31.24 times the percentage of residents getting insufficient sleep for the baseline state of Ohio, minus 107.87 YPLL plus 6.92 times the percent of residents getting insufficient sleep from the Ohio baseline equation for Illinois, minus 233.77 YPLL plus 6.7 times the percent of residents getting insufficient sleep from the Ohio baseline equation for Florida, and minus 317.65 YPLL minus 6.21 times the percent of residents getting insufficient sleep from the Ohio baseline equation for Tennessee.

Simplified, the equation for Illinois is -942.53 YPLL plus 38.16 times the percentage of residents getting insufficient sleep.

# Create the linear model with an interaction term
model3 <- lm(years_lost ~ insufficient_sleep * state, data = model3_data)

# Extract the equation
extract_eq(model3, use_coefs = TRUE, wrap = TRUE, coef_digits = 2, 
           operator_location = 'start', terms_per_line = 1)

\[ \begin{aligned} \operatorname{\widehat{years\_lost}} &= -834.66\\ &\quad + 31.24(\operatorname{insufficient\_sleep})\\ &\quad - 107.87(\operatorname{state}_{\operatorname{IL}})\\ &\quad - 233.77(\operatorname{state}_{\operatorname{FL}})\\ &\quad + 317.65(\operatorname{state}_{\operatorname{TN}})\\ &\quad + 6.92(\operatorname{insufficient\_sleep} \times \operatorname{state}_{\operatorname{IL}})\\ &\quad + 6.7(\operatorname{insufficient\_sleep} \times \operatorname{state}_{\operatorname{FL}})\\ &\quad - 6.21(\operatorname{insufficient\_sleep} \times \operatorname{state}_{\operatorname{TN}}) \end{aligned} \]

The Model Coefficients

For Ohio, the y-intercept is -834.66 YPLL (90% CI: -1068.1 - -601.23) and the slope is 31.24 YPLL per percent of residents with insufficient sleep (90% CI: 25.48-37.0). For Illinois, the y-intercept is -942.53 YPLL (90% CI: -1,294.8 - -590.25) and the slope is 38.16 YPLL per percent of residents with insufficient sleep (90% CI: 28.68-47.64). For Florida, the y-intercept is -1,068.43 YPLL (90% CI: -1,408.16 - -728.71) and the slope is 37.94 YPLL per percent of residents with insufficient sleep (90% CI: 29.64-46.43). For Tennessee, the y-intercept is -517.66 YPLL (90% CI: -874.32 - -159.7) and the slope is 25.03 YPLL per percent of residents with insufficient sleep (90% CI: 16.38-33.68). The confidence intervals for coefficients for all states besides Ohio include zero, so lines fitted for other states may not be meaningfully different from Ohio’s.

# Use tidy to extract the estimates, SE, and a 90% CI for model coefficients
tidy(model3, conf.int = TRUE, conf.level = 0.9) |>
  select(term, estimate, std.error, conf.low, conf.high) |>
  kbl(col.names = c('Term', 'Estimate', 'Std. Error', 
                    '90% CI Low', '90% CI High'), 
      digits = 2, align = 'lcccc', 
      caption = 'Model Coefficients') |>
  kable_classic(full_width = FALSE, 'striped')

Model Coefficients
Term	Estimate	Std. Error	90% CI Low	90% CI High
(Intercept)	-834.66	141.54	-1068.10	-601.23
insufficient_sleep	31.24	3.49	25.48	37.00
stateIL	-107.87	213.59	-460.14	244.41
stateFL	-233.77	205.98	-573.50	105.95
stateTN	317.65	216.64	-39.66	674.96
insufficient_sleep:stateIL	6.92	5.75	-2.56	16.40
insufficient_sleep:stateFL	6.70	5.14	-1.78	15.19
insufficient_sleep:stateTN	-6.21	5.25	-14.86	2.44

Summaries of Model Fit

The correlation between the percentage of county residents getting less than 7 hours of sleep per night and the years of potential life lost before the age of 75 per 100,000 people per year is 0.776. Using 352 counties to predict the premature mortality rate by the prevalence of insufficient sleep, the variance in this prevalence explains 60.3% (R² = 0.603) of the variation in premature mortality rate. The residual standard error of this model is 66.07 YPLL.

# Use glance to extract R2, RSE, and # of counties from model3
glance(model3) |>
  select(r.squared, sigma, nobs) |>
  mutate(correlation = sqrt(r.squared)) |>
  kbl(col.names = c('R-Squared', 'Residual Std Error', 
                    '# of Counties', 'Correlation'), 
      digits = c(3, 2, 0, 3), align = 'c', 
      caption = 'Model Fit Summaries') |>
  kable_classic(full_width = FALSE)

Model Fit Summaries
R-Squared	Residual Std Error	# of Counties	Correlation
0.603	66.07	352	0.776

Residual Analysis

This model conforms to all the assumptions of a linear model. The regression relationship is linear as no curve forms when plotting the residuals against the fitted values. The regression residuals overall show similar variance across all levels of the fitted values with no meaningful pattern. Finally, minus the major outlier from Florida, the residuals are well described by a normal model as demonstrated by the Q-Q plots by state.

# Augment model1 with the original data
model3_aug <- augment(model3, data = model3_data)

p1 <- ggplot(model3_aug, aes(x = .fitted, y = .resid)) +
  geom_point(aes(color = state), alpha = 0.5) +
  geom_smooth(method = 'lm', formula = y ~ x, se = FALSE, col = 'red') +
  geom_smooth(method = 'loess', formula = y ~ x, se = FALSE, col = 'blue') +
  scale_color_viridis_d() + 
  guides(color = 'none') + 
  labs(x = 'Fitted Values of YPLL', 
       y = 'Residual Values of YPLL', 
       title = 'Residual vs Fitted Values of YPLL', 
       caption = 'YPLL = years of potential life lost before age 75')

p3 <- ggplot(model3_aug, aes(x = .fitted, y = .resid)) +
  geom_point(aes(color = state), alpha = 0.5) +
  geom_smooth(method = 'lm', formula = y ~ x, se = FALSE, col = 'red') +
  geom_smooth(method = 'loess', formula = y ~ x, se = FALSE, col = 'blue') +
  scale_color_viridis_d() + 
  guides(color = 'none') + 
  facet_wrap(~ state) +
  labs(x = 'Fitted Values of YPLL', 
       y = 'Residual Values of YPLL', 
       title = 'Residual vs Fitted Values of YPLL', 
       caption = 'YPLL = years of potential life lost before age 75')

p2 <- ggplot(model3_aug, aes(sample = .resid)) +
  geom_qq(aes(color = state), alpha = 0.5) +
  geom_qq_line() +
  scale_color_viridis_d(name = 'State') + 
  facet_wrap(~ state) + 
  guides(color = 'none') + 
  labs(x = 'Expected Quantile', 
       y = 'Actual Value', 
       title = 'Q-Q Plot by State')

p1 + p2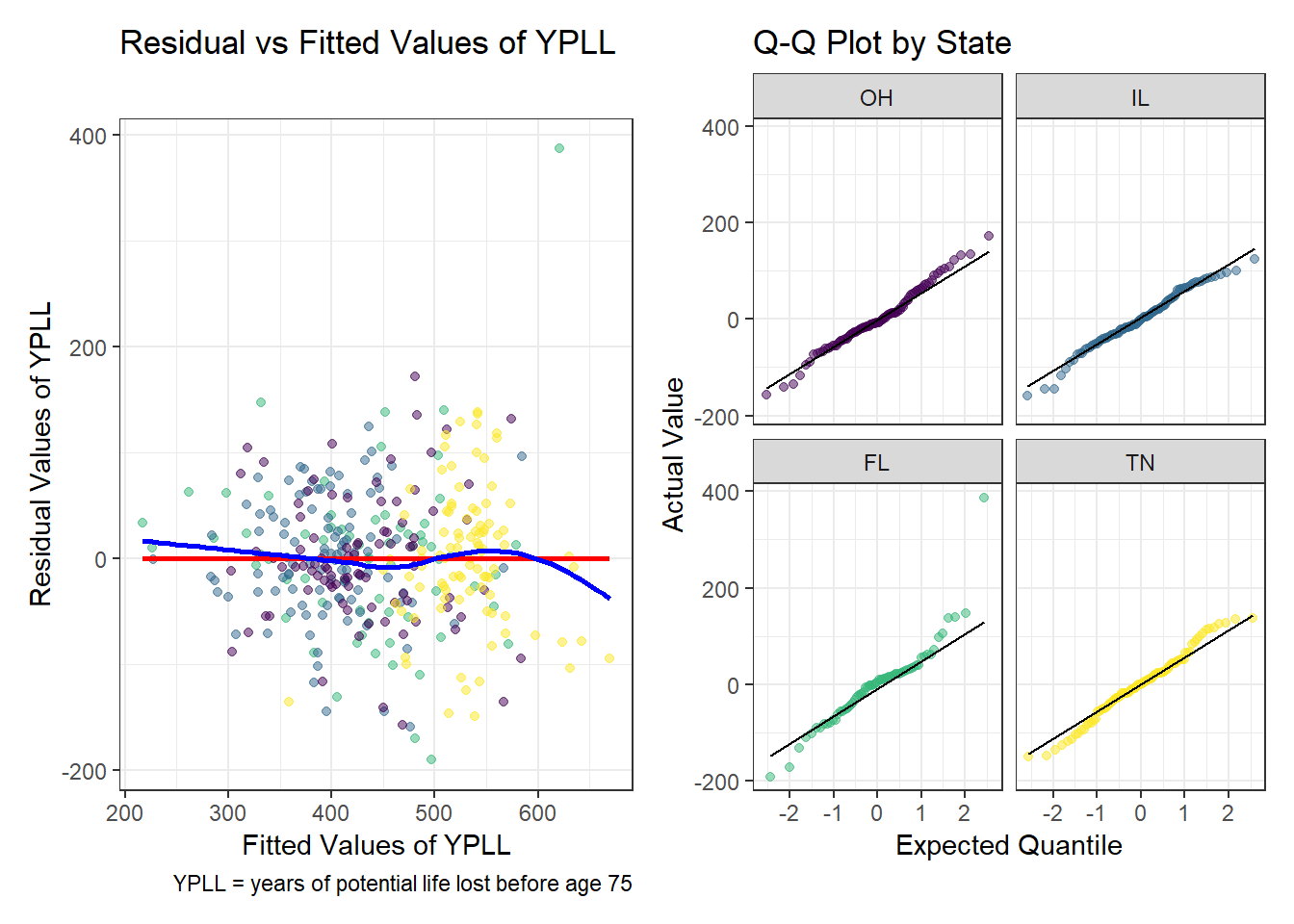

p3 + p2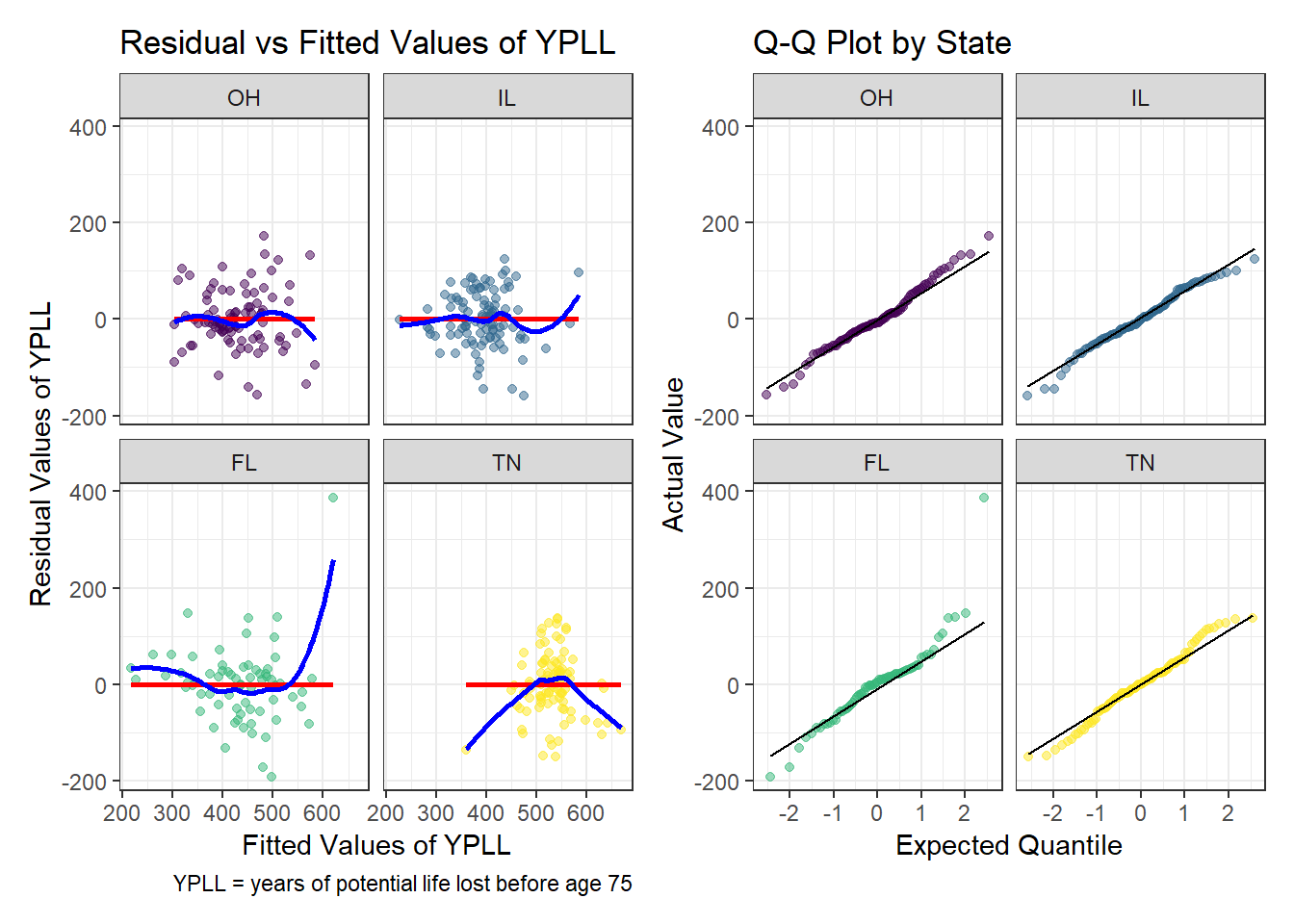

This model does not do well predicting the premature mortality rate in Cuyahoga County, Ohio by the percentage of residents experiencing insufficient sleep. The model’s fitted value is 566.54 YPLL as compared to the actual value of 431.16 YPLL, a residual of -135.37 YPLL.

# Select and display Cuyahoga County's stats from the augmented model
model3_aug |>
  filter(state == 'OH', county == 'Cuyahoga County') |>
  select(state, county, years_lost, .fitted, .resid) |>
  kbl(col.names = c('State', 'County', 'Actual', 'Fitted', 'Residual'), 
      digits = 2, align = 'llccc', 
      caption = 
        'Cuyahoga County, OH - Years of Premature Life Lost') |>
  kable_classic(full_width = FALSE)

Cuyahoga County, OH - Years of Premature Life Lost
State	County	Actual	Fitted	Residual
OH	Cuyahoga County	431.16	566.54	-135.37

Once again, Union County, Florida is the county with the least successful fitted value, with a residual of 386.64 YPLL. Broward County, Florida comes in second with a residual of -190.81 YPLL.

# Select and display the 2 counties with the worst residuals
model3_aug |>
  arrange(desc(abs(.resid))) |>
  select(state, county, years_lost, .fitted, .resid) |>
  head(2) |>
  kbl(col.names = c('State', 'County', 'Actual', 'Fitted', 'Residual'), 
      digits = 2, align = 'llccc', 
      caption = 
        'Least Successfully Fitted Counties') |>
  kable_classic(full_width = FALSE)

Least Successfully Fitted Counties
State	County	Actual	Fitted	Residual
FL	Union County	1007.13	620.49	386.64
FL	Broward County	306.15	496.96	-190.81

Conclusions and Limitations

Research shows that lack of sleep has a negative health impacts, so this model sought to quantify the additional burden in premature mortality rate, as measured by years of premature life lost before age 75 per 100,000 people per year, borne by residents of 352 counties in Ohio, Illinois, Florida, and Tennessee that have a higher percentage of residents who get less than 7 hours of sleep per night. This model predicts that a 1% increase in the prevalence of insufficient sleep is associated with an increase in premature mortality rate of 16.38-47.64 YPLL. Differences between state models may be due to chance since 90% confidence intervals all contain 0. States with lower baseline premature mortality burdens (Illinois, Florida, Ohio) tend to have a greater increase in risk of premature mortality (4-23%) with an increase in the prevalence of insufficient sleep than states with higher baseline premature mortality burdens (Tennessee; 2-16%), so public health initiatives on sleep may be less effective in populations already experiencing high premature mortality rates. This model and the food insecurity model from Analysis 1 both account for about 60% of the variation in premature mortality rates, and a 1% increase in predictor prevalence equates to an increase of about 30 YPLL in both. This model has negative y-intercepts (-1408.16 - -159.7 YPLL) while Analysis 1 predicts a positive baseline premature mortality rate (46.09-98.92 YPLL) regardless of the prevalence of food insecurity. Addressing lack of sleep may be cheaper and easier than addressing food insecurity, so based on the R², slope, and y-intercepts of this model, it predicts that reductions in the prevalence of insufficient sleep could be equally or more effective in reducing premature mortality risk than reducing food insecurity.

This model poses challenges to each level of inductive inference as outlined in Chapter 3 of The Art of Statistics by David Spiegelhalter (2021). One limitation of this model is that the prevalence of insufficient sleep is based on self-reporting, so this measure may not accurately reflect the true value of our sample. A second is that sample was not chosen at random. I did not randomly select counties, but also the survey establishing insufficient sleep is conducted by land-line phone dialing, which could bias our sample in favor of older adults who tend to get less sleep. Both threaten internal validity. Additionally, the sample has a higher density of counties with high prevalence of insufficient sleep as compared to the US distribution, so it has limited external validity.

Session Information

sessionInfo()

R version 4.2.2 (2022-10-31 ucrt)
Platform: x86_64-w64-mingw32/x64 (64-bit)
Running under: Windows 10 x64 (build 22000)

Matrix products: default

locale:
[1] LC_COLLATE=English_United States.utf8 
[2] LC_CTYPE=English_United States.utf8   
[3] LC_MONETARY=English_United States.utf8
[4] LC_NUMERIC=C                          
[5] LC_TIME=English_United States.utf8    

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
 [1] mosaicData_0.20.3  ggformula_0.10.2   Matrix_1.5-3       lattice_0.20-45   
 [5] forcats_0.5.2      stringr_1.5.0      dplyr_1.0.10       purrr_0.3.5       
 [9] readr_2.1.3        tidyr_1.2.1        tibble_3.1.8       tidyverse_1.3.2   
[13] naniar_0.6.1       janitor_2.1.0      kableExtra_1.3.4   ggrepel_0.9.2     
[17] ggplot2_3.4.0      patchwork_1.1.2    equatiomatic_0.3.1 broom_1.0.1       
[21] rmdformats_1.0.4   knitr_1.41        

loaded via a namespace (and not attached):
  [1] googledrive_2.0.0   colorspace_2.0-3    deldir_1.0-6       
  [4] ellipsis_0.3.2      ggridges_0.5.4      visdat_0.5.3       
  [7] htmlTable_2.4.1     ggstance_0.3.6      snakecase_0.11.0   
 [10] base64enc_0.1-3     fs_1.5.2            rstudioapi_0.14    
 [13] farver_2.1.1        bit64_4.0.5         fansi_1.0.3        
 [16] lubridate_1.9.0     xml2_1.3.3          mosaic_1.8.4.2     
 [19] splines_4.2.2       polyclip_1.10-4     Formula_1.2-4      
 [22] jsonlite_1.8.4      cluster_2.1.4       dbplyr_2.2.1       
 [25] png_0.1-8           ggforce_0.4.1       shiny_1.7.3        
 [28] compiler_4.2.2      httr_1.4.4          backports_1.4.1    
 [31] assertthat_0.2.1    fastmap_1.1.0       gargle_1.2.1       
 [34] cli_3.4.1           later_1.3.0         tweenr_2.0.2       
 [37] htmltools_0.5.4     tools_4.2.2         gtable_0.3.1       
 [40] glue_1.6.2          Rcpp_1.0.9          cellranger_1.1.0   
 [43] vctrs_0.5.1         nlme_3.1-160        svglite_2.1.0      
 [46] xfun_0.35           rvest_1.0.3         timechange_0.1.1   
 [49] mime_0.12           lifecycle_1.0.3     mosaicCore_0.9.2.1 
 [52] googlesheets4_1.0.1 MASS_7.3-58.1       scales_1.2.1       
 [55] vroom_1.6.0         hms_1.1.2           promises_1.2.0.1   
 [58] parallel_4.2.2      RColorBrewer_1.1-3  yaml_2.3.6         
 [61] curl_4.3.3          gridExtra_2.3       rpart_4.1.19       
 [64] labelled_2.10.0     latticeExtra_0.6-30 stringi_1.7.8      
 [67] highr_0.9           checkmate_2.1.0     rlang_1.0.6        
 [70] pkgconfig_2.0.3     systemfonts_1.0.4   evaluate_0.18      
 [73] labeling_0.4.2      htmlwidgets_1.5.4   bit_4.0.5          
 [76] tidyselect_1.2.0    magrittr_2.0.3      bookdown_0.30      
 [79] R6_2.5.1            generics_0.1.3      Hmisc_4.7-2        
 [82] DBI_1.1.3           mgcv_1.8-41         foreign_0.8-83     
 [85] pillar_1.8.1        haven_2.5.1         withr_2.5.0        
 [88] nnet_7.3-18         survival_3.4-0      modelr_0.1.10      
 [91] crayon_1.5.2        interp_1.1-3        utf8_1.2.2         
 [94] tzdb_0.3.0          rmarkdown_2.18      jpeg_0.1-10        
 [97] grid_4.2.2          readxl_1.4.1        data.table_1.14.6  
[100] reprex_2.0.2        digest_0.6.30       webshot_0.5.4      
[103] xtable_1.8-4        httpuv_1.6.6        munsell_0.5.0      
[106] viridisLite_0.4.1

Preliminaries

My Packages

Data Ingest

Data Development

Selecting My Data

Repairing the fipscode and factoring the state

Creating a Binary Categorical Variable

Creating a Multi-Category Variable

Revise order of variables

Three Important Checks

Missingness

Distinctiveness

Category Factor Completeness

Our Analytic Tibble

Printing My Tibble

Summarizing My Tibble

Saving My Tibble

Codebook

Table of States with County Counts

Table of Variables, Descriptions and Roles

Details on my Variables from CHR

Biggest Challenge

Analysis 1

The Variables

Research Question

Data Visualization

Transformation Assessment

The Fitted Model

The Prediction Equation

The Model Coefficients

Summaries of Model Fit

Residual Analysis

Conclusions and Limitations

Analysis 2

The Variables

Research Question

Data Visualization

The Fitted Model

The Prediction Equation

The Model Coefficients

Summaries of Model Fit

Prediction Analysis

Residual Plot

Prediction for Cuyahoga County, OH

My Two Least Successfully Fit Counties

Conclusions and Limitations

Analysis 3

The Variables

Research Question

Data Visualization

The Fitted Model

The Prediction Equation

The Model Coefficients

Summaries of Model Fit

Residual Analysis

Conclusions and Limitations

Session Information

Repairing the `fipscode` and factoring the `state`